Deconvolution Algorithms
Problem Statement
Formally, the task of deconvolution is to estimate the density function of the relevant quantity . Given are the measured density and the detector response function , the last of which is estimated from training data.
We investigate and develop algorithms which solve the deconvolution problem. The present web site is a bulletin for our scientific results and for our software.
Use Case—Cherenkov Astronomy
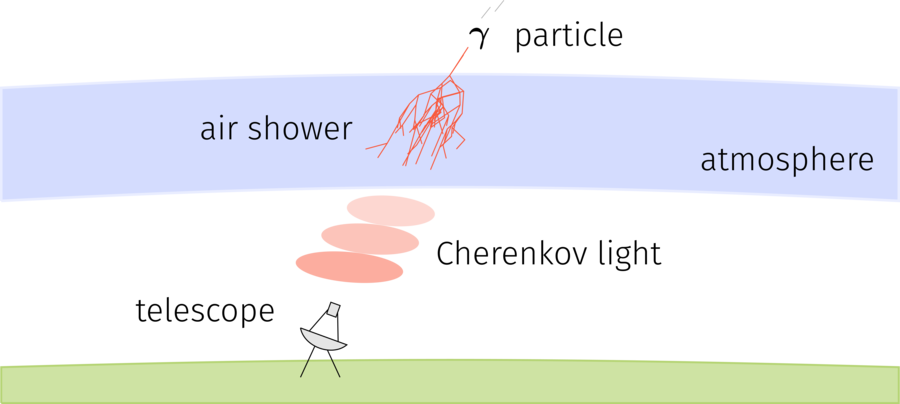
Cherenkov astronomy is a use case of deconvolution which studies the energy distribution of cosmic gamma radiation to reason about the characteristics of celestial objects. Since the gamma radiation is not directly measured by the ground-based telescopes employed in the field, deconvolution reconstructs the gamma particle distribution from the related Cherenkov light recorded by these telescopes.
Deconvolution algorithms are also applied in other areas of particle physics, for example at the LHCb experiment at CERN [2]. Another use case we see is the Manifesto Project, which studies the probability density of topics in political texts.
Providing Reference
We kindly ask you to provide reference to our DSAA paper.
@inproceedings{bunse2018unification,
author = {Bunse, Mirko and Piatkowski, Nico and Ruhe, Tim and Rhode, Wolfgang and Morik, Katharina},
title = {Unification of Deconvolution Algorithms for {C}herenkov Astronomy},
booktitle = {5th International Conference on Data Science and Advanced Analytics (DSAA)},
year = {2018},
pages = {21--30},
organization={IEEE}
}
Publications
-
M. Bunse, N. Piatkowski, T. Ruhe, W. Rhode, and K. Morik. Unification of deconvolution algorithms for Cherenkov astronomy. In Proc. of the 5th IEEE Int. Conf. on Data Science and Advanced Analytics (DSAA), pages 21-30, 2018.

-
M. Bunse, N. Piatkowski, and K. Morik. Towards a unifying view on deconvolution in Cherenkov astronomy. In Lernen, Wissen, Daten, Analysen (LWDA) conference proceedings, pages 73-77, 2018.

-
M. Bunse. DSEA rock-solid - regularization and comparison with other deconvolution algorithms. Master’s Thesis, TU Dortmund, 2018.

Supplementary Material
Software
The Julia package CherenkovDeconvolution.jl and examples are hosted on GitHub. The package implements the investigated algorithms:
- DSEA+, our enhanced version of the Dortmund Spectrum Estimation Algorithm
- RUN, the Regularized Unfolding [3]
- IBU, the Iterative Bayesian Unfolding [4]
A native port of this package to Python, called CherenkovDeconvolution.py, is under current development. Our experiments are implemented in a separate repository.
Bibliography
- C. Bockermann, K. Brügge, J. Buss, A. Egorov, K. Morik, W. Rhode, and T. Ruhe. Online analysis of high-volume data streams in astroparticle physics. In Proc. of the ECML-PKDD 2015, pages 100-115, 2015.
- T. Ruhe, M. Schellenberg, and B. Spaan. Application of the Dortmund spectrum estimation algorithm to LHCb monte carlo simulations. Tech Report, SFB 876, 2018.
- V. Blobel. An unfolding method for high energy physics experiments. In Adv. Stat. Techniques in Part. Phys., pages 258-267, 2002.
- G. D’Agostini. Improved iterative Bayesian unfolding. arXiv:1010.0632, 2010.
- T. Ruhe, M. Börner, M. Wornowizki, et al. Mining for spectra - the Dortmund spectrum estimation algorithm. In Proc. of the ADASS XXVI, 2016.
- N. Milke, M. Doert, S. Klepser, D. Mazin, V. Blobel, and W. Rhode. Solving inverse problems with the unfolding program TRUEE: Examples in astroparticle physics. In Nucl. Instrum. Methods Phys. Res. A, Vol. 697, pages 133-147, 2013.
- T. Ruhe, K. Morik, and the IceCube Collaboration. Development of a general analysis and unfolding scheme and its application to measure the energy spectrum of atmospheric neutrinos with IceCube. In Eur. Phys. J. C, Vol. 75, 2015.
Share your ideas with us!
 Mirko Bunse
Mirko Bunse
We are always looking for comments, criticism, and for collaborators. Can we count you in? :)
mirko.bunse [ät] cs.tu-dortmund.de
You may also like our work on simulation data mining.

